Новости

« вернуться к списку

версия для печати

Математик представил наглядное доказательство теоремы Пифагора

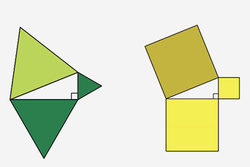
Иллюстрация с сайта www.lenta.ru Математик Андрес Навас из Университета де Сантьяго де Чили представил очередное простое и наглядное доказательство теоремы Пифагора. Посвященный исследованию препринт автор опубликовал на сайте arXiv.org.

Теорема Пифагора утверждает, что в прямоугольном треугольнике (то есть треугольнике с прямым углом) квадрат гипотенузы (самой большой стороны, располагающейся напротив прямого угла) равен сумме квадратов катетов (двух отличных от гипотенузы меньших сторон). В настоящее время известно более 350 различных доказательств этого утверждения.

Навас использует теорему Бойяи — Гервина, которая утверждает равносоставленность двух любых равновеликих многоугольников. Ученый совершает два поворота треугольника АВС: первый — вокруг точки А на угол 60 градусов против часовой стрелки, второй —вокруг точки В на 60 градусов по часовой стрелке. Затем Навас рассчитывает площадь образовавшегося многоугольника, составленного из двух многоугольников, площади которых равны площади треугольника АВС, и равностороннего треугольника со стороной с, откуда и выводит требуемое утверждение.

Теорема Пифагора, как утверждает в своей книге "Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции" нидерландский математик и историк науки Бартель ван дер Варден, была известна еще в XVIII веке до нашей эры жителям Вавилона, а также индийцам и египтянам. Широкую известность она получила после публикации 13 книг "Начал" Евклида, где в конце первой книги формулируется и доказывается теорема Пифагора.

источник: Lenta.ru

Последние материалы раздела

• 30 декабря 2016
  На орбите Земли Новый год отметят 16 раз
• 30 декабря 2016
  В забайкальской школе из-за невыплаты зарплаты массово уволились учителя
• 30 декабря 2016
  Рособрнадзор запретил прием студентов в пять вузов
• 30 декабря 2016
  Россия в I квартале 2017 года планирует выполнить не менее четырех космических пусков
• 30 декабря 2016
  Карякин стал чемпионом мира по блицу

Обсуждение

Добавить комментарий

Обсуждение материалов доступно только после регистрации.

« к началу страницы